Применение дифференциала
Ряд Тейлора теорема для функции одной переменной
Если у функции f: U ⊂ R → R существуют непрерывные производные до степени k+1 в окрестности точки a, тогда её можно представить с помощью следующего ряда:
f(a+h) = f(a) + f'(a)⋅h + f''(a)⋅h2/2 + f(k)(a)⋅hk/k! + Rk(a,h)
где limh→0Rk(a,h)/hk = 0
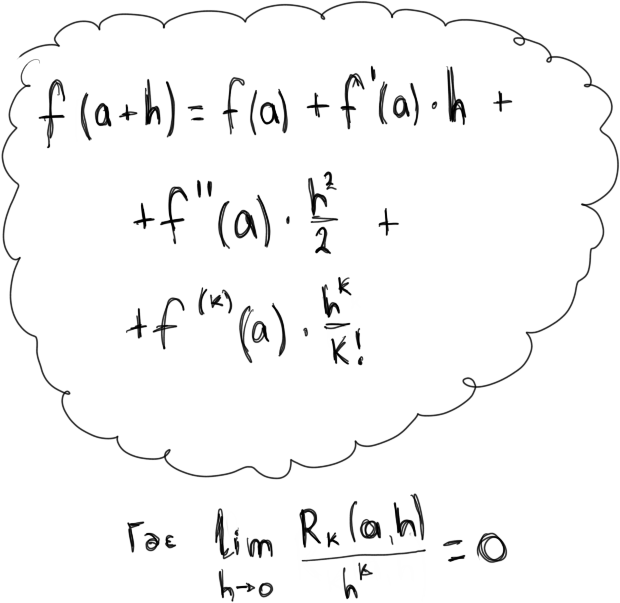
Ряд Тейлора первой степени
Пусть дана функция f : U ⊂ Rn → R, которая дифференируема в точке a. Ряд Тейлора первой степени для переменной h=(h1,...,hn)
P1(a+h) = f(a) + Σni=1[hidf/dxi(a)]
Ряд Тейлора второй степени
Пусть дана функция f : U ⊂ Rn → R, которая дифференируема в точке a до второй степени. Ряд Тейлора второй степени будет иметь вид:
P2(a+h) = f(a) + Σni=1[hidf/dxi(a)] + ½Σni=1Σnj=1[hihjd2f/(dxidxj)(a)]

Экстремум функции
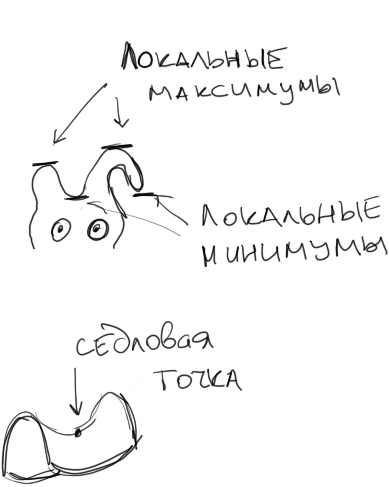
Пусть дана функция f:U ⊂ Rn → R при x ∈ U. Точка x0 является локальным максимумом функции, если f(x0)≤f(x) в некоторой окрестности вокруг точки x0. Точка x0 является локальным минимумом функции, если f(x0)≥f(x) в некоторой окрестности вокруг точки x0.
Пусть дана функция f: U ⊂ Rn → R дифференируемая в точке x0 и точка x0 является локальным экстремумом, то x0 является критической точкой, т.е. ∇f(x0)=0, поэтому все частные производные первого порядка в данной точке равны нулю.
Если все частные производные равны нулю, то точка x0 не обязательно является критической точкой, а может быть седловой точкой.
Гессиан функции
Пусть дана функция f: U ⊂ Rn → R принадлежащая второму классу. Матрица Гессе f в точке x0 это симметричная матрица:
d2f/dx1dx1(x0) ... d2f/dx1dxn(x0) Hf(a) = ... ... ... d2f/dxndx1(x0) ... d2f/dxndxn(x0)

Гессиан функции f в точке x0 это следующая функция:
Hf(x0)(h) = ½(h1 ... hn)⋅Hf⋅(x0)⋅(h1 ... hn)T
Пусть дана функция f : U ⊂ Rn → R, f ∈ C3 и U является открытым интервалом. Рассмотрим критическую точку x0 ∈ U (∇f(x0)=0):
x0 является точкой локального минимума, если Hf(x0)(h) > 0 для любого h ≠ 0.
x0 является точкой локального максимума, если Hf(x0)(h) < 0 для любого h ≠ 0.
x0 является седловой точкой, если Hf(x0)(h) ≠ 0 для любого h ≠ 0.
Множетели Лагранжа
Данный метод был введён для решения задачи нахождения точек экстремума на закрытом множестве D. Описаные выше методы подходят для нахождения экстремума на открытом множестве, поэтому проблема разбивается на две: первая - найти экстремумы в открытом интервале, вторая - найти экстремумы на границе интервала, сравнив полученные экстремумы, мы найдём экстремумы функции на множестве D.
Введём понятие поверхность уровня, поверхность уровня функции f - это множество точек пространства, в которых функция равна заданному значению, Вы могли это видеть ранее, например, в картах, где изолиниями обозначена высота над уровнем моря, каждая такая изолиния - это поверхность уровня. Поверхность уровня h это множество точек f(xi, ...) = h
Пусть даны две функции первого класса f : U ⊂ Rn → R и g : U ⊂ Rn → R. Точка a ∈ U и g(a) = c и поверхность уровня "с" функции g обозначим S. Если функция fs в точке a является максимумом или минимумом, то ∇g(a) будет перпендекулярна S в точке a, что означает, что существует некое число λ такое, что ∇f(a)=λ∇g(a).
Пример
Необходимо найти максимум и минимум функции f(x,y,z) = x + 2y + 3z на участке образованном пересечением цилиндра x2 + y2 = 2 и плоскости y + z = 1
В данном примере мы имеем ограничение двумя функциями, поэтому множителей будет 2, в общем виде нас интересует результат:
∇f(x,y,z)=λ∇g(x,y,z)+μ∇h(x,y,z)
где g(x,y,z) = x2 + y2 - 2 и h(x,y,z) = y + z - 1
более подробно:
df/dx = λ⋅dg/dx + μ⋅dh/dx
df/dx = λ⋅dg/dy + μ⋅dh/dy
df/dx = λ⋅dg/dz + μ⋅dh/dz
решив данную систему уравнений, получим две критические точки: P(1,-1,2) и Q(-1,1,0), что бы проверить, какая из них является максимумом, а какая минимумом, необходимо вычислить значение функции:
f(1,-1,2) = 5
f(-1,1,0) = 1
Следовательно, максимум находится в точке P, минимум - в точке Q.
