Вероятность
Вероятность, что подброшенная монета упадёт орлом вверх 50%, что при броске шестигранного кубика выпадет 4 - 16,7%, что завтра на кого-нибудь упадёт метеорит - 0.00000000294%. Это простые примеры, достаточно разделить количество желаемых событий на общее количество случаев и мы получаем вероятность события, но когда результаты эксперимента могут быть не только орлом или решкой (что эквивалентно да/нет), а большим набором данных. Например, вес батона хлеба, если мы возьмём в магазине 1000 буханок хлеба и взвесим каждую, то мы узнаем, что на самом деле батон не весит 400 грамм, результаты будут варьироваться в диапазоне 384-416 грамм (допуск разброса веса предусмотрен ГОСТом). Если Вы построите график "Количество буханок - Вес", то график будет иметь форму напоминающую колокол, что-то похожее на следующий график:
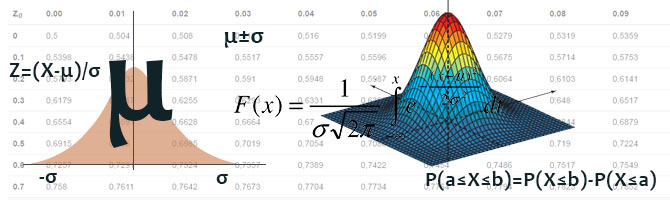
Плотность вероятности нормального распределения

Такую форму график получит потому, что большинство значений близко к 400. Это - пример нормального распределения, множество событий имеют закон нормального распределения, например, вес или рост для определённого возраста, или среднее время Вашего похода до магазина и многие другие события также подчиняются закону нормального распределения.
В случае таблицы Вы имеете дело с дискретными данными, т.е. для каждого веса есть определённая вероятность, но в случае графика дело немного меняется, теперь мы говорим не о 1000 буханок, которые мы взвесили, а обо всех буханках в мире сразу! Зачем? Что бы не взвешивать все буханки. Имея закон распределения, который мы получили взвесив 1000 буханок (мы могли взвесить 100, 200, 500, сколько угодно), мы можем предположить, что сколько бы мы буханок не взяли, замерив их, мы получим ту же форму колокола. Используя термины статистики, все буханки хлеба - это генеральная совокупность, 1000 замеренных буханок - выборка.
Теперь, возьмём одну буханку хлеба, какова вероятность, что её вес будет между 390г и 400г?
Вероятность события между a и b:
P(a ≤ X ≤ b) = P(X ≤ b) - P(X ≤ a)
Распределение вероятности - это функция, в которой для каждого события Х присваивается вероятность p, что событие произойдёт
Распределение Гаусса
Нормальное распределение получило своё название абсолютно справедливо: по статистике, большинство событий происходят именно с вероятностью нормального распределения, но что это значит? Это означает, например, что когда Вы видите на упаковке хлеба обозначение "Вес: 400±16г" - вес батона имеет нормальное распределение со средним значением 400г и стандартным отклонением 16г.
Таблица нормального распределения
Таблица нормального распределения - это затабулированные значения функции нормального распределения.
Для нахождения вероятности события Z0 можно воспользоваться таблицей нормального распределения ниже. На пересечении строк (n) и столбцов (m) находится значение вероятности n+m.
| Z0 | 0.00 | 0.01 | 0.02 | 0.03 | 0.04 | 0.05 | 0.06 | 0.07 | 0.08 | 0.09 |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.500 | 0.504 | 0.508 | 0.512 | 0.516 | 0.520 | 0.524 | 0.528 | 0.532 | 0.536 |
| 0.1 | 0.540 | 0.544 | 0.548 | 0.552 | 0.556 | 0.560 | 0.564 | 0.568 | 0.571 | 0.575 |
| 0.2 | 0.579 | 0.583 | 0.587 | 0.591 | 0.595 | 0.599 | 0.603 | 0.606 | 0.610 | 0.614 |
| 0.3 | 0.618 | 0.622 | 0.625 | 0.629 | 0.633 | 0.637 | 0.641 | 0.644 | 0.648 | 0.652 |
| 0.4 | 0.655 | 0.659 | 0.663 | 0.666 | 0.670 | 0.674 | 0.677 | 0.681 | 0.684 | 0.688 |
| 0.5 | 0.692 | 0.695 | 0.699 | 0.702 | 0.705 | 0.709 | 0.712 | 0.716 | 0.719 | 0.722 |
| 0.6 | 0.726 | 0.729 | 0.732 | 0.736 | 0.739 | 0.742 | 0.745 | 0.749 | 0.752 | 0.755 |
| 0.7 | 0.758 | 0.761 | 0.764 | 0.767 | 0.770 | 0.773 | 0.776 | 0.779 | 0.782 | 0.785 |
| 0.8 | 0.788 | 0.791 | 0.794 | 0.797 | 0.799 | 0.802 | 0.805 | 0.808 | 0.811 | 0.813 |
| 0.9 | 0.816 | 0.819 | 0.821 | 0.824 | 0.826 | 0.829 | 0.832 | 0.834 | 0.837 | 0.839 |
| 1 | 0.841 | 0.844 | 0.846 | 0.849 | 0.851 | 0.853 | 0.855 | 0.858 | 0.860 | 0.862 |
| 1.1 | 0.864 | 0.867 | 0.869 | 0.871 | 0.873 | 0.875 | 0.877 | 0.879 | 0.881 | 0.883 |
| 1.2 | 0.885 | 0.887 | 0.889 | 0.891 | 0.892 | 0.894 | 0.896 | 0.898 | 0.900 | 0.901 |
| 1.3 | 0.903 | 0.905 | 0.907 | 0.908 | 0.910 | 0.911 | 0.913 | 0.915 | 0.916 | 0.918 |
| 1.4 | 0.919 | 0.921 | 0.922 | 0.924 | 0.925 | 0.926 | 0.928 | 0.929 | 0.931 | 0.932 |
| 1.5 | 0.933 | 0.934 | 0.936 | 0.937 | 0.938 | 0.939 | 0.941 | 0.942 | 0.943 | 0.944 |
| 1.6 | 0.945 | 0.946 | 0.947 | 0.948 | 0.950 | 0.951 | 0.952 | 0.953 | 0.954 | 0.955 |
| 1.7 | 0.955 | 0.956 | 0.957 | 0.958 | 0.959 | 0.960 | 0.961 | 0.962 | 0.963 | 0.963 |
| 1.8 | 0.964 | 0.965 | 0.966 | 0.966 | 0.967 | 0.968 | 0.969 | 0.969 | 0.970 | 0.971 |
| 1.9 | 0.971 | 0.972 | 0.973 | 0.973 | 0.974 | 0.974 | 0.975 | 0.976 | 0.976 | 0.977 |
| 2 | 0.977 | 0.978 | 0.978 | 0.979 | 0.979 | 0.980 | 0.980 | 0.981 | 0.981 | 0.982 |
| 2.1 | 0.982 | 0.983 | 0.983 | 0.983 | 0.984 | 0.984 | 0.985 | 0.985 | 0.985 | 0.986 |
| 2.2 | 0.986 | 0.986 | 0.987 | 0.987 | 0.988 | 0.988 | 0.988 | 0.988 | 0.989 | 0.989 |
| 2.3 | 0.989 | 0.990 | 0.990 | 0.990 | 0.990 | 0.991 | 0.991 | 0.991 | 0.991 | 0.992 |
| 2.4 | 0.992 | 0.992 | 0.992 | 0.993 | 0.993 | 0.993 | 0.993 | 0.993 | 0.993 | 0.994 |
| 2.5 | 0.994 | 0.994 | 0.994 | 0.994 | 0.995 | 0.995 | 0.995 | 0.995 | 0.995 | 0.995 |
| 2.6 | 0.995 | 0.996 | 0.996 | 0.996 | 0.996 | 0.996 | 0.996 | 0.996 | 0.996 | 0.996 |
| 2.7 | 0.997 | 0.997 | 0.997 | 0.997 | 0.997 | 0.997 | 0.997 | 0.997 | 0.997 | 0.997 |
| 2.8 | 0.997 | 0.998 | 0.998 | 0.998 | 0.998 | 0.998 | 0.998 | 0.998 | 0.998 | 0.998 |
| 2.9 | 0.998 | 0.998 | 0.998 | 0.998 | 0.998 | 0.998 | 0.999 | 0.999 | 0.999 | 0.999 |
| 3 | 0.999 | 0.999 | 0.999 | 0.999 | 0.999 | 0.999 | 0.999 | 0.999 | 0.999 | 0.999 |
| 3.1 | 0.999 | 0.999 | 0.999 | 0.999 | 0.999 | 0.999 | 0.999 | 0.999 | 0.999 | 0.999 |
| 3.2 | 0.999 | 0.999 | 0.999 | 0.999 | 0.999 | 0.999 | 0.999 | 0.999 | 0.999 | 1.000 |
| Таблица 1. Таблица нормального распределения. Красным выделены часто используемые значения при выборе критической области | ||||||||||
Нормальное распределение - среднее 0 и отклонение 1?
Не только. График нормального распределения построен для среднего значения ноль и стандартного отклонения единица, т.е. 0±1. Но если Ваши среднее и отклонение отличаются от нуля и единицы, то к Вашим услугам следующая формула:
Z = (X - μ) / σ
Где μ и σ - среднее значение и стандартное отклонение для Вашего распределения соответственно, а X - величина, для которой Вы хотите узнать вероятность. Возвращаясь к примеру с батоном хлеба - для того, что бы узнать, какова вероятность, что батон будет весить меньше 396 грамм - необходимо подставить в формулу значения X=396, μ = 400, σ = 16:
Z = (396 - 400) / 16 = -0.25
Далее, по таблице необходимо найти значение для Z. Как для Z = -0.25, так и для Z = 0.25 это будет 0,5987 (нормальное распределение симметрично, поэтому значение вероятности определяется для абсолютного значения Z: график симметричен относительно оси Y, поэтому значение вероятности не зависит от знака X)
Свойства функции распределения
- Симметрична относительно центра (среднее значение - математическое ожидание μ)
- Мода и медиана равны математическому ожиданию μ
Функция распределения
Функция распределения предназначена для того, что бы определить, какова вероятность, что величина X меньше или равна некоторого числа x.
На примере батона из первого абзаца: если мы хотим узнать, какова вероятность, что батон будет весить меньше 410 грамм, то, воспользовавшись формулой приведения, получим Z=0.63 и значение P(X<0.63) = 0,7357, т.е. вероятность того, что батон будет весить 410 грамм или меньше - 73,57%

Среднее значение нормального распределения (μ)
Математическое ожидание (среднее значение) для стандартного нормального распределения равно нулю: μ = 0
Нормальное распределение в excel
Что бы получить значение нормального распределения в эксель, существует формула "НОРМ.РАСП" (в старых версиях НОРМРАСП), в которую передаётся значение события X, например, какова вероятность попасть в интервал [-0.5;0.5]?
=НОРМРАСП(0,5;0;1;1) = 0,35
=НОРМ.РАСП(0,5;0;1;1) = 0,35
Синтаксис команды следующий: НОРМРАСП(событие Х, среднее, отклонение, интегральная). Так, Вы можете найти значение нормального распределения без приведения значений:
=НОРМ.РАСП(396;400;16;1) = 0.4
Для поиска значения Z, при наличии вероятности, например, для 95%, можно воспользоваться формулой "НОРМОБР":
=НОРМОБР(0,95;0;1) = 1,64