Закон распределения
Пример закона распределения
Закон подлости - это закон распределения, но у него пока нет математической модели, зато у многих других законов есть достаточно чёткое математическое описание, например, у нормального закона распределения или у распределения Пуассона. Распределение, функция распределения, закон распределения - это всё одно и то же, математическое описание вероятности события. Например, по дороге на работу Вы иногда заходите в лавку купить воды, для Вас это просто магазин, а у лавочника уже лежит закон распределения и лавочник знает, когда Вы зайдёте и сколько воды закупить на неделю! Вот как он это сделал:
| ПН | ВТ | СР | ЧТ | ПТ | СБ | ВС | ||
| 1 | × | ✓ | ✓ | ✓ | ✓ | ✓ | × | |
| 2 | × | × | × | ✓ | ✓ | × | × | |
| 3 | × | ✓ | × | × | ✓ | ✓ | ✓ | |
| 4 | ✓ | ✓ | ✓ | × | × | ✓ | ✓ | |
| 5 | × | ✓ | ✓ | × | × | × | ✓ | |
| 6 | ✓ | ✓ | × | × | ✓ | × | × | |
| 7 | × | ✓ | ✓ | × | ✓ | ✓ | ✓ | |
| 8 | × | × | × | × | × | ✓ | ✓ | |
| 9 | × | ✓ | × | ✓ | ✓ | × | × | |
| 10 | ✓ | ✓ | ✓ | × | × | ✓ | ✓ | |
| 11 | × | ✓ | ✓ | ✓ | × | × | ✓ | |
| 12 | × | ✓ | × | × | × | ✓ | ✓ | |
| 13 | × | × | ✓ | ✓ | ✓ | × | ✓ | |
| 14 | ✓ | × | ✓ | ✓ | × | ✓ | ✓ | |
| 15 | ✓ | × | × | ✓ | × | × | ✓ | |
| 16 | × | × | × | × | × | ✓ | × | |
| 17 | × | × | ✓ | × | × | × | × | |
| 18 | ✓ | ✓ | × | ✓ | ✓ | × | ✓ | |
| 19 | ✓ | × | ✓ | × | × | ✓ | ✓ | |
| 20 | × | × | ✓ | ✓ | × | × | × | |
| 21 | × | ✓ | × | ✓ | ✓ | ✓ | × | |
| 22 | × | × | ✓ | ✓ | × | × | ✓ | |
| 23 | ✓ | × | ✓ | × | ✓ | × | × | |
| 24 | × | × | ✓ | × | ✓ | × | × | |
| 25 | ✓ | ✓ | ✓ | × | ✓ | × | × | |
| 26 | ✓ | × | × | ✓ | ✓ | × | ✓ | |
| 27 | × | × | ✓ | ✓ | ✓ | × | ✓ | |
| 28 | × | × | × | × | ✓ | ✓ | ✓ | |
| 29 | ✓ | × | × | × | × | ✓ | × | |
| 30 | × | ✓ | ✓ | ✓ | × | × | ✓ |
В первую очередь лавочник составил таблицу, когда вы покупали воду и когда не покупали, затем эти данные записал в таком виде, что видно сколько раз в неделю вы заходили:
| количество посещений | |||||||
|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 0 | 2 | 5 | 8 | 9 | 6 | 0 | 0 |
| количество недель | |||||||
Итак, всего было 30 недель и можно говорить об относительных цифрах, то есть, выразить в процентах количество посещений:
Виды представления
| количество посещений | |||||||
|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 0% | 6.7% | 16.7% | 26.7% | 30% | 20% | 0% | 0% |
| недели с таким количеством посещений | |||||||
Эта таблица - закон распределения количества посещений в неделю. Также, этот закон может выглядеть в виде красивого графика:
Также можно было бы вывести уравнение, которое описывает это распределение, и это уравнение также было бы законом распределения.
Таблица, график и уравнение - это способы представления одного и того же: какова вероятность события X. Лавочнику интересно знать, с какой вероятностью Вы зайдёте 0,1,2 и т.д. раз, поэтому событие X - это количество посещений в неделю и закон распределения даёт вероятность этого события.
В жизни
Таким образом собиралась информация о различных событиях во всех уголках мира: сколько муравьёв живёт в муравейнике, с какой скоростью сгорает вещество, средний заработок по стране и так далее. Затем начали замечать, что разные события (событие - это интересующий нас факт) имеют одинаковые графики закона распределения, например, рассматривая работу телефонной станции в течение года выяснилось, что закон распределения звонков в минуту имеет следующий вид:
Здесь, например, вероятность, что в течение минуты позвонит 4 человека - 17.55%, вероятность, что позвонит 2 человека - 8.42%, вероятность, что позвонят 5 человек или меньше - 61.6%.
Выдвижение гипотез
А теперь, имея распределение вероятности, мы можем делать различные предположения, например, в случае с телефонной станцией, мы можем выдвинуть предположение, что для того, что бы обслужить 87% звонков, нам необходимо отвечать на 7 звонков в минуту (вероятность, что позвонит 7 человек и меньше - 86.6%, мы округлили). Что бы обслужить 93% звонков, нам необходимо отвечать на 8 звонков в минуту и так далее.
Лавочник может предположить, что если он будет закупать 4 бутылки воды в неделю, то вероятность, что воды не будет, когда она Вам понадобится - 20%, в свою очередь, вероятность, что воду он продаст не всю - 50.1%.
Закон распределения дискретной величины
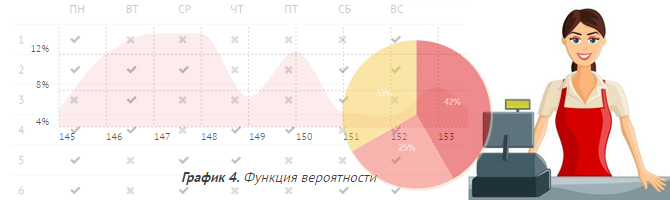
Рассмотренные примеры имеют дискретный вид, т.е. событие X имеет определённые значения. Случается, что дискретное распределение не подходит, что необходимо говорить о диапазонах значений, например, если Вы будете замерять количество воды в стакане: Вы замеряете не количество атомов, а объём, при этом всегда есть погрешность, если вы замерили 99.92 мл, то это может быть 99.925, или 99.922365, или 99.25552323 и так далее, так вот, что бы не включать все эти значения в таблицу вы включаете только округлённое значение и в итоге опять получаете таблицу, график или функцию:
| Закон распределения | |
|---|---|
| Объём воды | Вероятность |
| 145 мл | 3.5% |
| 146 мл | 12.3% |
| 147 мл | 8.9% |
| 148 мл | 2.6% |
| 149 мл | 15.2% |
| 150 мл | 14.1% |
| 151 мл | 4.8% |
| 152 мл | 13.4% |
| 153 мл | 14.5% |
| 154 мл | 2.2% |
| 155 мл | 8.7% |
Закон распределения в виде графика, теперь это не дискретные значения, как в таблице, это примерное представление о том, сколько на самом деле воды в стакане. Если мы хотим узнать, какова вероятность, что воды в стакане 150 мл - мы должны посчитать вероятности всех значений между 149.5 и 150.5, что равно площади графика между 149.5 и 150.5 (если Вы не понимаете почему - изучите интегралы). Логично, что площадь под конкретным значением будет бесконечно малой, поэтому и вероятность какого-либо конкретного события будет нулевой.
Итак, для дискретных распределений мы строим таблицы, для остальных - графики, размещённая слева таблица не совсем корректна, поскольку в реальности мы заполняем огромную таблицу с конкретными значениями, без округлений, а затем строим график, но без сомнений такая таблица может быть использована для понимания процесса.
Термины!
Может возникнуть некоторая путаница в терминах:
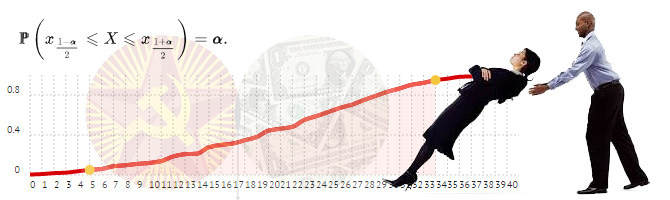
Функция вероятности - функция, у которой на входе значение Х, а на выходе вероятность события Х;
Функция распределения - функция, у которой на входе значение X, а на выходе вероятность событий меньше или равных X;
Плотность вероятности - функция вероятности.
Как составить закон распределения
Теперь Вы знаете, что для того, что бы составить закон распределения, необходимо собрать данные и оформить их в виде графика (или таблицы, если речь идёт о дискретных величинах). Составление закона распределения - это результат сбора статистических данных, далее этот закон используется для принятия решений.
- Собрать данные
- Представить данные в числовом виде
- Упорядочить данные
Используемые законы распределения
На данный момент существует огромное множество законов распределений, без сомнений, распределение Гаусса (нормальное распределение) - самое популярное, поскольку описывает любое "нормальное" событие, также, на производстве и сфере услуг часто используется распределение Пуассона, например, в теории очередей или как в примере про телефонную станцию.